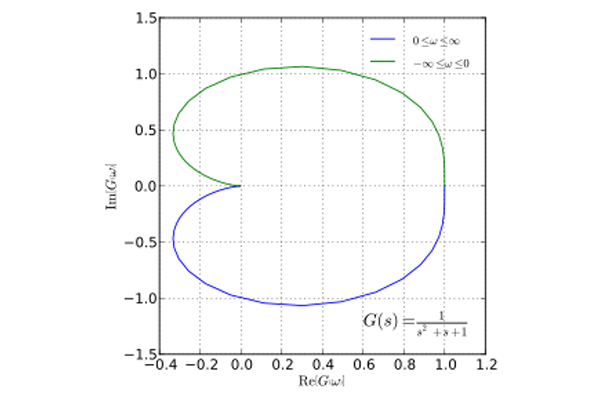
معیار ثبات nyquist
شرایط ثبات به راحتی با قضیه محاصره nyquist قابل مشاهده است. مثالی در شکل 13.17 نشان داده شده است. یک نقشه معمولی بخش درون فاز یا واقعی 1 + H را بر روی محور x و قسمت چهارم فاز در محور y ارائه می دهد. هنگامی که 1 + H با افزایش فرکانس در جهت عقربه های ساعت ، از محور واقعی عبور می کند ، ثبات نیاز به افزایش H در شکل 13.16 از بیشتر از 1-دارد هنگامی که H = −1 ، یک ورودی سینوسی پاسخ بی نهایت را مجبور می کند. این وضعیت به ثبات حاشیه ای گفته می شود زیرا خروجی فقط در صورت وجود ورودی اجباری سینوسی رشد می کند. هنگامی که H <−1 ، خروجی حتی بدون ورودی رشد می کند. هرچه مقدار H در هنگام عبور از محور واقعی منفی باشد ، سرعت رشد سریعتر خواهد بود.
کاربرد این اصل باعث می شود بی ثباتی و بی ثباتی حاشیه ای مانند مثال های زیر به صورت گرافیکی نشان داده شود.
روغن کاری هیدرودینامیکی
در سریال Tribology ، 1990
اتصال متقاطع در سختی اما در میرایی نیست
سپس شرایط ثبات به صورت زیر نوشته می شود:
اگر همه Ai مثبت باشند ، ممکن است آخرین شرط به شکل زیر باشد:
جایی که α ، β و δ ضرایب مثبت هستند.
هنگامی که ضرایب میرایی مستقیم همه مثبت هستند ، که این امر برای یک تحمل ژورنال صادق است ، و هنگامی که شرایط برای ثبات استاتیک برآورده شود ، برای هر مقدار M ثبات تضمین می شود به شرط آنکه: یعنی ،
از آنجا که نسبت همیشه از 0.25 کوچکتر است ، این شرایط ثابت می کند که نسبت به حالت استاتیک محدود کننده تر از حالت استاتیک است. بنابراین ، وجود میرایی مستقیم باعث به خطر انداختن ثبات بی قید و شرط تحمل می شود. با این حال یاتاقان با کاهش جرم تثبیت می شود.
وقتی یک اصطلاح مستقیم میرایی منفی می شود ، این حرکت همیشه ناپایدار نیست ، اما محدودیت های مقادیر ضرایب مربوطه محدود کننده تر از وضعیت قبلی است.
فرمول بندی و محدودیت های مختلط: روش های کامل زمینه
O.C. Zienkiewicz ، … J.Z. زو ، در روش اجزاء محدود: مبانی و اصول آن (چاپ هفتم) ، 2013شرایط پایداری که در بخش 9.3 به دست آمده است. (9.18)] برای مشکلات دو میدانی ، که بعداً در Eq استفاده کردیم. (9.32) برای فرم کشش ساده مخلوط ، هنگام تقریب سه میدان فرم ارائه شده در Eq ، باید اصلاح شود. (9.35) در نظر گرفته شده است.
بسیاری از مشکلات دیگر در یک گروه مشابه قرار می گیرند (به عنوان مثال ، خم شدن صفحه) و از این رو شرایط ثبات به طور کلی مفید هستند. الزام اکنون این است
ε
این اولین بار در Ref. [24] و به طور مستقیم از معیار دو میدانی مطابق شکل زیر پیروی می کند.
سیستم Eq. (9/35) با افزودن معادلات سوم به دوم ، با ثابت بودن دلخواه ، می توان «تنظیم» شد. الان داریم
استفاده از اولین مورد فوق
از نیاز دو میدانی [معادله. (9.32)] نتیجه می گیرد که ما نیاز داریمبرای اینکه سیستم معادله راه حلی داشته باشد.
برای ایجاد شرط دوم ، Eq را دوباره تنظیم می کنیم. (9.35) به عنوان
ε
این می تواند دوباره با اضافه کردن ضرب ها و سوم از معادلات فوق به ترتیب اول و دوم تنظیم شودما در مورد جزئیات تقریبی هر یک از تقریب های احتمالی به این بحث نمی پردازیم
ε
– فرمول بندی یا تست های متصل مربوط به آنها به عنوان آرگومان شبیه به مشکلات دو میدان است.
در بعضی از کاربردهای عملی از شکل سه میدانی ، تقریب معادلات دوم و سوم در (33/9) به طور مستقیم برای از بین بردن کلیه موارد به جز جابجایی استفاده می شود. این منجر به شکل خاصی از روش جابجایی می شود که به آن فرم (-bar) گفته شده است [25،26]. در شکل ، مشتقات تابع شکل با تقریبهای حاصل از فرم مخلوط جایگزین می شوند. ما باید این مفهوم را با نمونه ای از ماده تقریباً غیر قابل فشرده در بخش 10.4 نشان دهیم. دولت متعادل
ساده ترین معادله ای که می تواند پویایی روابط را در یک شبکه مبتنی بر تئوری تعادل هایدر توضیح دهد ، است
وضعیت پایداری یک سیستم در حالت نهایی آن جایی است که همه پیوندها در آن قرار دارند | xij | ≈ 1 و xij dxij / dt> 0؛ xij به 1 افزایش می یابد یا به 1 کاهش می یابد. با توجه به اینکه محصولات توابع Θ یکی است ، r.h.s. در معادله در لینک های مثبت 7+ و در لینک های منفی 1 است. بنابراین این پیکربندی است nyquist